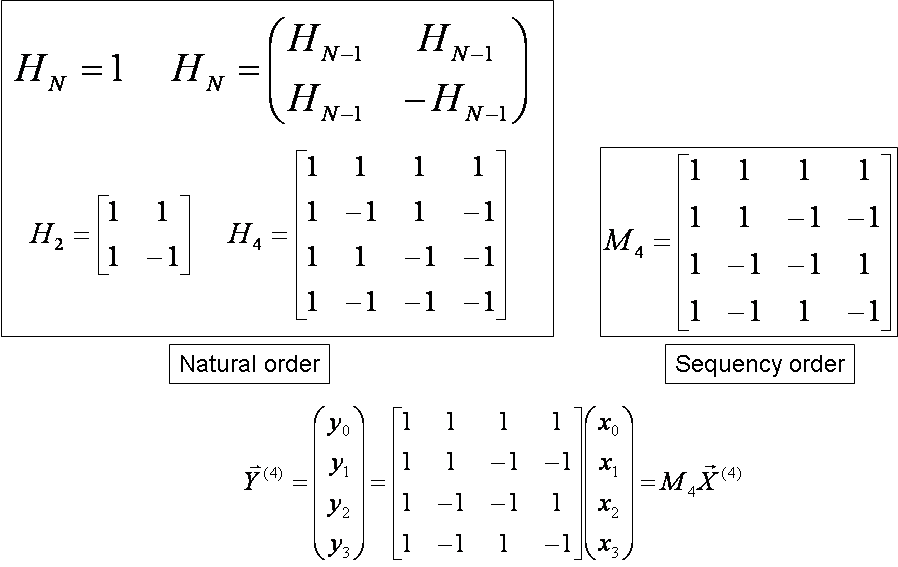Fast algorithm for Walsh Hadamard transform on sliding windows

Wanli Ouyang and Wai-Kuen Cham

Abstract��This paper proposes a fast algorithm for Walsh Hadamard Transform on sliding windows which can be used to implement pattern matching most efficiently. The computational requirement of the proposed algorithm is about 1.5 additions per projection vector per sample, which is the lowest among existing fast algorithms for Walsh Hadamard Transform on sliding windows.

This webpage introduces the fast Walsh Hadamard transform algorithm of the following paper:

Wanli Ouyang and Wai-Kuen Cham, "Fast algorithm for Walsh Hadamard transform on sliding windows", IEEE Trans. Pattern Analysis and machine Intelligence, 32(1):165-171, Jan. 2010. [Full text^*] [Powerpoint

]

* Personal use of these materials is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works must be obtained from IEEE.

Introduction (from Wikipedia)

The Walsh Hadamard transform (WHT), also known as the Hadamard transform, Hadamard-Rademacher-Walsh transform, Walsh transform, or Walsh-Fourier transform, is an example of a generalized class of Fourier transforms. It is named for the French mathematician Jacques Solomon Hadamard, the German-American mathematician Hans Adolph Rademacher, and the American mathematician Joseph Leonard Walsh. It performs an orthogonal, symmetric, involutional, linear operation on $2 m$ real numbers (or complex numbers, although the Hadamard matrices themselves are purely real).

The Hadamard transform H_N is a 2^m x 2^m matrix, the Hadamard matrix (scaled by a normalization factor), that transforms N=2^m real numbers into 2^m real numbers.

Fig. 1 WHT in natural order and sequency order.

Application of WHT

In computer vision, it is used in pattern matching, road/path tracking , mouth tracking , wide baseline image matching, scene labeling, texture synthesis and augmented reality.

WHT is also used in data encryption, as well as many signal processing and data compression algorithms, such as HD Photo and MPEG-4 AVC. In video compression applications, it is usually used in the form of the sum of absolute transformed differences.

WHT is used in Quantum computation. As pointed out in Wikipedia, many quantum algorithms use the Hadamard transform as an initial step.

The Nlog(N) fast WHT algorithm

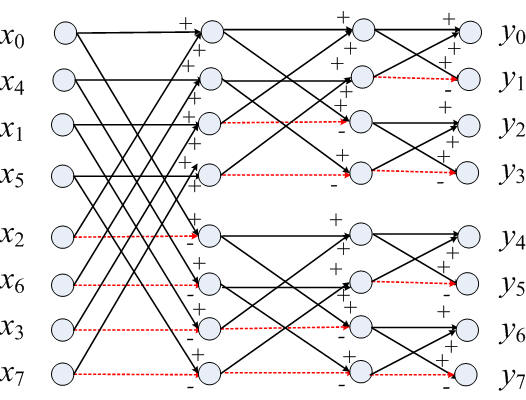
Naive implementation of the WHT would have a computational complexity of O( $N$ $2$ ). The fast WHT algorithm as show in Fig. 2 requires only $N log N$ additions or subtractions. One of these algorithms is in [a].

Fig. 2 The fast Walsh Hadamard transform applied to a vector of length 8 (From Wikipedia).

The 1.5N-1 fast WHT algorithm -- This paper

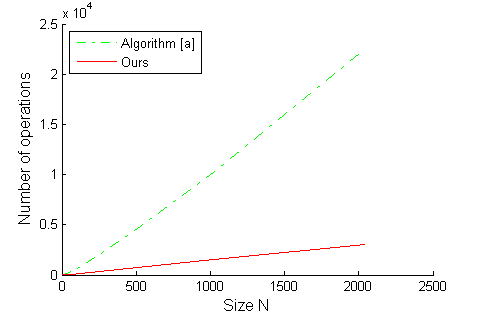
This paper proposes a fast algorithm for Walsh Hadamard Transform on sliding windows which can be used to implement pattern matching most efficiently. The computational requirement of the proposed algorithm is about 1.5 additions per projection vector per sample. The proposed algorithm requires 1.5N-1 additions for transforming N numbers into N real numbers. A comparison of our proposed algorithm and the algorithm in [a] is shown in Fig. 3.

Other famous WHT algorithms on sliding windows are in [b][c]. In [d], we propose a new transform and its fast algorithm.

Fig. 3 The number of operations as a function of the WHT transform size N for the algorithm in [a] and our algorithm.

New paper is here [f], about 1.33N additions for WHT.

Experimental results (where is my cup?)

The proposed fast WHT algorithm is utilized for pattern matching. The algorithm finds out the same result as Full search (exhaustive search) and significantly saves the computation required.

In the following video (enable ActiveX control to see the video), pattern matching the proposed algorithm requires lees than 0.1 second to locate the cup using pattern matching. The experiment considers image without noise and image with Gassian noise, Image blur and JPEG compression disturbances. This algorithm guarantees to find the global optimum in pattern matching application.

ACKNOWLEDGMENTS

Many introduction of WHT and fast WHT algorithm in this webpage are directly copied from Wikipedia. To avoid annoyance, we did not provide reference to Wikipedia for all places.

[a] Fino, B.J., and Algazi, V.R., 1976, "Unified Matrix Treatment of the Fast Walsh-Hadamard Transform," IEEE Transactions on Computers 25: 1142-1146.

[b] Y. Hel-Or and H. Hel-Or, "Real Time Pattern Matching Using Projection Kernels," IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 27, no. 9, pp. 1430-1445, Sept. 2005.

[c] G. Ben-Artzi, H. Hel-Or, and Y. Hel-Or, "The Gray-Code Filter Kernels," IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 29, no. 3, pp. 382-393, Mar. 2007.

[d] Wanli Ouyang, Renqi Zhang and Wai-Kuen Cham, "Fast pattern matching using orthogonal Haar transform ", In Proc. IEEE CVPR 2010, Webpage and source code.

[e] Wanli Ouyang, Federico Tombari, Stefano Mattoccia, Luigi Di Stefano, and Wai- Kuen Cham, "Performance Evaluation of Full Search Equivalent Pattern Matching Algorithms, " IEEE Trans. Pattern Anal. Mach. Intell., 34(1):127-143, Jan. 2012. Webpage and source code

[f] Wanli Ouyang and Wai-Kuen Cham, "Segmented Gray-Code Kernels for Fast Pattern Matching", IEEE Trans. Image Processing, 22(4):1512-1525, Apr. 2013. Webpage and source code

Source code

Matlab code is available here. The code is in C using Visual studio 6.0 as the compiling environment.

Please note the "Conditions of Use and Disclaimer" below for this code.

^{Conditions of
Use and Disclaimer:

You are only granted a limited right to use this software for your

personal non-commercial use.

This software is provided as SHAREWARE for testing and evaluating

purposes and cannot be sold or used in any commercial way, or

distributed, with or without consideration and whether on its own or

bundled with any commercial package, or by accompanying books, magazines

or any publication in any media without express written permission from

the owner.

The owner of this software accepts no responsibility for any damages

resulting from any use relating to this software and makes no warranty

or representation, either express or implied,
including but not limited

to, any implied warranty of merchantability or fitness for a particular

purpose. This software is provided "AS IS", and you, as a limited
right

user, assume all risks when using it.

This software is intended for personal non-commercial use only.

For any other use of the code, whether commercial or otherwise, please make

enquiries by writing to:

Technology Licensing Office

The Chinese University of Hong Kong

Shatin, N.T., Hong Kong

Email: tech_license@cuhk.edu.hk}